This page is part of multiple pages about robot configuration and usage. Please choose the robot tag to see an overview.
At the core of this page is to explain firmware concepts. Details about the data storage is in the object model page.
¶ Forward and inverse kinematics
The original procedure to calculate kinematics by Jacobian is replaced by screw theory with geometric algebra means.
Procedure of development:
- calculate forward from all angle combinations with a high sample number by DH or with existing RRF kinematics code
- calculate all inverse solutions (up to 8 for 6 axis robot)
- verify that one of the inverse solutions is the forward angle combination (to make sure that all inverses were calculated)
- verify all inverse solutions by calculating forward for each of them
- calculate forward with DH and with screw based code and verify that the result is the same (this verifies the DH-screw converter as well)
- all calculations must tolerate some rounding errors in the range of 1e-6 (which is 1 micrometer)
¶ G-Code to machine position

The CAM creates a G-Code file, which uses letters like G1 XYZAC or G1 XYZABCD with different meaning. XYZ are cartesian coordinates in mm, while AC (or BC, AB, ABCD) are degrees values.
Note: IJK mode is problematic, because it conflicts with G2/G3 IJ parameters, so it can only be used with G0/G1.
The firmware interpretes the letters in kinematics as input values. Kinematics can translate it at it's will, can combine, calculate with them, ignore them etc. For a meaningful interpretation, it needs to know what the CAM means by A letter e.g. The match is often done by convenience, but it is more safe to define the match explicitly by specifying P"mapDriveLetterDn=...". It is also possible that the match is not 1:1, but more motors used than letters in G-Code used.
Firmware kinematics than outputs its calculation results into machine positions and the main firmware positions the motors and prints or drills at the commanded motor positions.
¶ orientationType
Hardware (3D printer, CNC) and Software differ in how many orientation axes are supported, the possibilities are:

If red is the direction of the X axis, green of Y axis and blue of the Z axis, with Z pointing up or down, the possibilities of orientation are from left to right:
- no orientation: only position is specified. An example is a cartesian printer with the hotend always pointing into one direction
- Z axis orientation: only Z axis orientation is specified. The direction of X and Y axis is unspecified and can change and is out of control for the printer/CNC. Examples are 5 axis printers or CNC of different types like AC, BC mounted on table or head.
- full orientation: all axes' orientations are under control. The axes vectors are orthonormal and righthanded, i. e. vector lengths are 1 each and all vertical on each other.
The fact that 5 axis AC printers/CNC doesn't use all 6 axes is the reason for not supporting full orientation mode. This is sufficient in most cases (the drill orientation of the CNC is not important, as it rotates fast). But in other cases like a concrete printer, a hotend where orientation follows the printing path would be an advantage.
¶ Orientation storing
Rotations and the resulting orientation can be stored by different methods. Two subtypes can be divided by whether the angle changes are infinitesimal (all angles are changed at the same time) or one-after-another, where the order of changing axis is important:
Infinitesimal angle changes, all at once, order arbitrary:
- rotation matrix with 3x3 values, storing three 3-dimensional vectors, stores the orientation best, but needs most memory.
- quaternions store full orientation with 4 parameters: one parameter stores the rotation angle, 3 parameters the rotation axis
- skew symmetric storing also needs 4 (or 3) parameters, the rotation axis, and the rotation angle must be stored separately
- Axis-angle: Euler axis and angle.
Skew and Axis-Angle can be in two forms both: using unit vectors and the rotation angle as separate value or the unit vector multiplied with the angle. The result are 4 or 3 values.
Angle changes one-after-another, order is important:
- processing of Denavit-Hartenberg rotations
- Euler angles exist in 12 subtypes and store rotation angles, which are executed in a specific order
Euler angles are not used in robot kinematics code, because they have problems at edges like gimbal lock. They are however often used, e.g. in aviation as roll-pitch-yaw (RPY).
¶ Transformation matrix
Orientation and position can be stored in different form and different amount of parameters. One often used method is the transformation matrix with 4 rows and 4 columns. The last row is always (0,0,0,1), to the amount of to-be-stored parameters is 12.
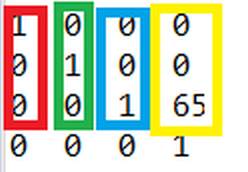
The left coloured 3x3 submatrix is the rotation matrix, the yellow the positional information.
It contains the following information:
- X axis direction as XYZ vector in first column (red). (1 0 0) means the X axis is directed into X direction. (0 0 -1) would mean, the X axis directs to down (negative Z)
- Y axis (green) is the orientation of the Y axis
- Z axis (blue) is the orientation of the Z axis
- position XYZ (yellow) is the information about the tool tip's position
Some technical information about the transformation matrix:
- rotation matrix: for every orientation vector, x² + y² + z² = 1, the same is true for every row of the 3x3 rotation submatrix.
- each orientation vector is vertical to the other ones (orthonormal) and the axes are organized righthanded. As a result the determinant of the 3x3 left upper matrix is 1 (lefthanded would be -1).
- full can be uniquely translated into quaternions and reverse. Quaternions are used for storage efficiency, using 4 instead of 9 values. They can also be translated into angle-axis mode with 4 parameters, where axis is a Euler axis (not to be confused with Euler angles) and angle is the rotation around this axis.
- The four numbers (0 0 0 1) in the last line make sure that rotations and translations stay at their positions (they would make non-linear affine transformations if other values are used). They don't change.
- the transformation matrices are created by Screw or Denavit-Hartenberg parameters and multiplied to get forward kinematics
¶ World coordinate or workpiece mode
This chapter is relevant if using
- CNC 5 axis
- 4 axis palletized with object on the robot plate
For forward and inverse kinematics calculations it is important to set world or workpiece mode. Default is world mode.
- workpiece mode (in gaming also called model space, object space) desribes transformations from the view of the workpiece
- world mode (in gaming called world space) describes transformations with world coordinates
When the workpiece is rotated or moved itself, calculating in workpiece mode for a part of the chain is necessary.
Examples for workpiece mode is CNC 5 axis with rotary axes on the table like Open5x and 4 axis palletized with the print object installed on the robot endpoint and the hotend stationary outside the robot. Example configurations are provided in the robot type documents about CNC 5 axis and 4 axis palletized.
Workpiece mode means that the transformation matrices need to be multiplied in back order. I was a bit suprised, that I could invert the ZYX rotation matrix (which is represented by one Dn definition) directly by inverting it. I expected that I have to change rotation/transformation order from ZYX to XYZ before inverting, but it is not the case, as A-1B-1 = (BA)-1, so X-1Y-1Z-1=(ZYX)-1, so it's sufficient to invert ZYX.
The inversion of a tranformation matrix looks like this:
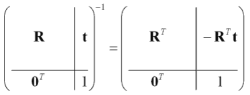
T are transposes, R is the rotation matrix, t is the position matrix.
It is important to get the transformation matrix order for multiplication correct, i. e. the order of the Dn definitions, because matrix multiplication order is not commutative, i. e. A * B is different from B * A. In case of changing from world mode to workpiece mode, the transformation matrix must
- be inverted by setting D!n
- change the Dn order to be reversed for the workpiece Dn-s
Example: D0 to D2 are BC settings for the rotary axes of CNC 5 axis BC. The workpiece is assembled on the C plate, then changing to workpiece mode means inverting by using D!0, D!1, D!2. For the other Dn values of the linear axes and tool Dn, the normal order is used, D3 to D6 in this example.
¶ Angle-Axis
Full orientation can be described by Euler axis and an angle around this axis.
Please see https://en.wikipedia.org/wiki/Euler%27s_rotation_theorem
¶ Quaternions
Quaternions are numbers of one real and three imaginary numbers, developed by Hamilton in 19th century, and can describe spatial rotations.
- the real number describes the rotation angle around an axis
- the three imaginary numbers describe the axis
A typical number looks like q0 + q1i + q2j + q3k, where ijk are imaginary numbers.
By using a calculation named Slerp, interpolation between two quaternions is unambigious and the orientation change has constant velocity, which is advantageous for constant extrusion, contrary to Euler angles. Slerp is often used in 3D gaming development.
Online translator to convert between rotation matrix and quaternion I use are https://www.andre-gaschler.com/rotationconverter/ and https://www.energid.com/resources/orientation-calculator (both show real number last for quaternions).
A nice introduction video to quaternions is https://www.youtube.com/watch?v=mHVwd8gYLnI
¶ Slerp
For segmentation of a rotation, simply dividing angles (e. g. Euler angles) is not the correct way, because the resulting segmented rotations have nonlinear velocity. The method called Slerp, which is based on quaternions, assures constant angle change and velocity of rotation.
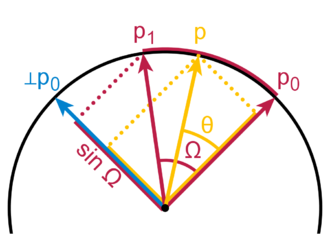
(from Wikipedia https://en.wikipedia.org/wiki/Slerp).
The simple method would be to divide the line between p0 and p1 for segmentation (tendon). With slerp, the curve of the circle is divided instead.
Slerp is used in Kinematics for
- segmentation of a long move to avoid snapping into different work modes
- calculating jacobian matrix in full orientationType mode
Interpolations to calculate segments are implemented by using Slerp with introduction see https://en.wikipedia.org/wiki/Slerp and implementation based on Shoemake https://dl.acm.org/doi/pdf/10.1145/325165.325242
Firmware code follows the code of https://www.euclideanspace.com/maths/algebra/realNormedAlgebra/quaternions/slerp/index.htm
¶ Degrees of freedom, rank
Forward kinematics result in X, Y, Z and orientation. Together they result in 6 parameters, which correspond to 6 degrees of freedom (DOF). A 6 axis robot can create those 6 DOFs. Every configuration of less than 6 actuators is limited in the creation of the result.
Examples of reduced rank:
- a cartesian printer has 3 DOFs: control over X, Y, Z positions, but no control about the orientation of the endpoint. By mechanical means, the endpoint is always vertical.
- CNC 5 axis has 5 DOFs: X, Y, Z positions and control over the orientation of the Z axis, but no control over the orientation of the X and Y axes. A CNC spindle doesn't need X, Y axis orientation control (they constantly change).
- singularity situations of a 6 axis robot: in one of the singularity situations, position and orientation changes are limited. For singularity types, see singularity section.
¶ Workspace and Singularities
Workspace is the space where an object can be reached by the robot. Calculation is a combination of position and orientation. Positions near the edges should be avoided, because rotations of axes become critical and movement precision is reduced.
(image from https://www.mdpi.com/2218-6581/9/2/27/htm)
Singularities are unreachable robot positions or positions where movement results are undefined. Approaching singularities is also probelmatic, because some angle velocities are approaching infinity. See a good overview of singularities for 6 axis robots here.
Being in a singularity may be necessary when homing. In Example 2 of the DH parameter explanation, the homing position is in a singularity (a small movement of most of the axes result in massive X movement and minimal Z movement). Setting the stepper positions by homing may be a necessity. A solution is to home and set the positions, then moving specific axes with G1 H2 to a position where the robots positions are outside the singularity, then proceed. Those G1 H2 moves can be placed into the homing file.
To avoid printing in a singularity, M208 can be set accordingly. Please see the chapter about M208 for details.
Singularities are solved by calculating generalized inverses.
¶ Working modes
For part of the robot types, a specific cartesian position and orientation can be reached by different arm positions. https://docs.duet3d.com/User_manual/Machine_configuration/Configuration_five_bar_parallel_scara chapter "Working Modes" explains it for 5 bar parallel scara. An industrial 6 axis robot has up to 8 possible angle combinations for a given position and orientation.
Crossing the boundaries and changing the working modes is only possible by crossing singularities. For exceptions please see below.
To avoid problems, the working mode can be specified by telling the firmware using a set of actuator angles with P"workmode=..." as reference, which is used as beginning position/orientation to calculate targets. Default are the homing angles. The calculation uses a print path which is solvable the whole path, i. e. all segments of a move will be achievable with limited velocity of the actuators. When the kinematics is informed about a new move, the method LimitPosition is called which checks whether the position and orientation is reachable. The decision is made by the M208 limits and the inverse kinematics calculation whether the robot can reach the position and orientation. The calculation stays inside the work mode, starting from the position/orientation of the stored angles in cachedAngles.
The following methods exist to specify workmode:
- home uses the homing values and 0 until all values are specified
- current uses the current prismatic and rotary actuator positions
- a list of values specify mm (prismatic) or degree (rotary) values. If a value is left empty, it uses the current set value
To change workmode, additional G-Code commands like G1 H2 moves are necessary and setting to the new workmode. An alternative is to cross the singularity with the experimental solution to set velocity for critical actuators to 0 and cross the singularity. This will often produce inexact print or drill results, but may be acceptable.
¶ Speed and Acceleration control
Speed control is managed directly in the inverse kinematics: the calculated needed angle velocities are compared against the M203 setting and a violation reported if it exceeds the limit. The limits are defined as degrees/min for rotational axes and mm/min for prismatic ones. The overall speed should be controlled by limiting the extrusion speed by the core RRF, but I'll test it.
Acceleration and jerk is not monitored in this release.
Near and at a singularity, the angular speed of a single or few actuators would grow to infinity and stop printing. The solution is to avoid singularities or to set those angular speed to 0 and accept some inaccuracy. The affected segments are corrected and the surrounding ones smoothing down to velocity values approaching 0 to avoid jerks. The M203 and M201 (and maybe M566) settings are used as upper angular velocity limits for each actuator.
The setting P"violationBehaviour=..." controls what to do with violations (e. g. warn, hinder movement, accept x % over with warning). This is handled together with angle violations.
¶ Tool offsets and orientation
Tool offsets are defined by G10 X, Y, Z offsets. There are no parameters for tool orientation in G10 (a proposal would be to add IJK)*), so a modification of the DH parameters directly is needed, if the tool itself is not vertical. When changing tools with a toolchanger, each tool could have it's own tilt values.
The X, Y, Z offset values are added to the tool's coordinate system. A positive Z offset with a coordinate system pointing down (coordinate system's Z axis is vector (0 0 -1), pointing down) will lower the distance between hotend and bed e.g.
The tool offset is added to the kinematics chain (the last Dn transformation matrix) before a forward kinematics is calculated. Every change of G10, a tool change eg., is immediately effective.
¶ Letters cartesian vs axis
Some Drive and G-Code Letters have different meanings, depending on context:
- cartesian coordinates of XYZUVW in mm position or distance
- orientation AB, BC, AC in degrees, IJK tool vector in radians
- drive letters like XYZUVWABC as reference for a specific actuator/stepper
In G-Code the two meanings are mixed unhappily, some examples:
- normal G1 X Y Z A B => X, Y, Z movements with A B rotations (5 axis CNC) or IJK for using vector tools
- G1 H2 X Y Z U V W => movements of single motors
- G31 X Y Z => X, Y, Z distances
- G10 X Y Z => offsets from reference
- M92, M203, M566, M201, M906 XYZUVW => stepper letter related
- M574 X, Y, Z => stepper letter related
¶ double vs float variables
Tests with forward, inverse kinematics and angle calculations resulted in differences of e-04 at worst between float and double precision variables for 6 axis robot calculations of positions and orientations. It seems acceptable to use float, because it needs less memory and can run on all newer Duet hardware with single and double precision Cortex chips (all M4F and M7 based with FPU. M7 offers double precision FPU on 6HC and 6XD).
Technical details:
- float uses its 32 bits for: 1 bit for sign, 8 bits for exponent and 23 bits for mantissa/fraction/coefficient. The 23 bits are 2-bit based, which mean 7...8 decimal digits precision (2^23 about 10 mio)
- double uses its 64 bits: 1 bit for sign, 11 bits for exponent and 52 bits for mantissa, which means about 15...16 decimal digits precision.
¶ Firmware development and compilation
For installation and running robot kinematics, taking the binaries is the easiest solution. The following is only interesting if one wishes to compile or change something static inside the firmware code (e.g. using more than 6 axes).
For indidivual compilation of source, the guide https://github.com/Duet3D/RepRapFirmware/wiki/Building-RepRapFirmware should be followed. For the robot, a github fork is made and the code added to the branch 3.5-dev
The direct path is https://github.com/JoergS5/RepRapFirmware/tree/3.5-dev/src/Movement/Kinematics
The file contents are as follows
- RobotKinematics.h contains all declarations and variables
- RobotKinematics.cpp contain the kinematics API methods which are used by core RRF
- RobotKinematics1.cpp contains all code which can run and be tested outside RRF
- RobotKinematics2.cpp contains code to calculated the generalized inverse. It can run and be tested outside RRF
- RobotKinematics3.cpp contains code to help configuration reading and setting. It can run and be tested outside RRF
Additional steps:
- Kinematics.h and .cpp the variables robot and include RobotKinematics.h are added. robot is used instead of robot5axis to use K13
- Config/Pins.h set SUPPORT_ROBOT to 1 and all other Kinematics SUPPORT... to 0
- all .h and .cpp files with names starting with RobotKinematics in folder src/Movement/Kinematics
If it doesn't compile or with many errors, I may have forgot to change WINDOWSMODE 1/RRMODE 0 to WINDOWSMODE 0/RRFMODE 1 in RobotKinematics.h when checkin into github. The values are used to set Windows or RRF environment.
¶ setup analysis, logDetailed
If the results of calculations are not as expected, the reason can be a wrong Dn setup of angles or distances. To check every Dn's result, the log level can be set to logDetailed. Every move result will be output to the console with detailed information about the rotation matrices: positions and orientations. This allows to check whether the joint angle results are as expected. The Jacobian and Generalized inverse will be logged also, so unusual angle velocities can be detected.
Calculation starts at a cached matrix of the last move. If the new move is segmented and a short segment, only a few iterations are needed and will be logged, until the target is reached. Long moves will be segmented into large segments with reduced precision and only the last segment is with high precision. Long moves may log too many details to be informative.
Long unsegmented moves happen
- when in simulation mode
- first check of firmware by calling LimitPosition to check whether the target is reachable
- G0 moves
- segmentation is turned off
The long unsegmented moves are calculated in chunks of large segments to avoid "snap of angles" into different work modes and because the Jacobian - Inverse method is working for small angle changes only.
Short segmented moves happen
- G1, G2, G3 moves with segmentation activated
- the move itself is short
¶ segmentation
When RRF receives a long G1 move or a G2/G3 move, it will be segmented. Segmentation means, a long line or curve is divided into short straight lines. Similar to how Pi is calculated by approaching the curve by smaller and smaller line approximations.
For 3D printing, typical values are 0.1 or 0.2 mm line segments. For CNC, 0.01 mm are typical values. Smaller values mean better quality of the approximation, but more processor power needed. If too much power is needed, it will show up in M122 hiccup values.
The segments can be created by the CAM/slicer also.
Segmentation in RRF has the following advantages
- smaller G-Code file and lower SD card transfer speed requirement
- lower G-Code overhead, as every G-Code command needs resources like LimitPosition calculation, and movement planning
- RRF tries to balance actuator speeds between the segments, so the movements will be smoother
Disadvantages
- CAM/slicer may have special functionality like collision avoidance which can be considered in G-Code if CAM segments
- faster pause/stop because the moves are shorter
¶ Joint types
Robot kinematics supports different joint types, configured by P"axisTypes=...".
There are 6 common types, currently supported are:
- R revolute, also called rotational and hinge joints. It changes position and orientation.
- P prismatic, also called linear, sliding. It changes only position.
- p for the passive rotational joint, where the position is defined by a parallelogram, the p parameter is added.
- spherical, indirectly supported by 3 rotational joints: a roll-pitch-yaw (RPY) construction of three rotational joints of a 6 axis industrial robot behaves like a spherical joint. A spherical joint (and hence the RPY 3 axes) suffer from the gimbal lock singularity, which occurs at a 6 axis robot when axis 5 is 0 degrees and the axes 4 and 6 are parallel.
The other types are helical, cylindrical and universal.
¶ testing kinematics
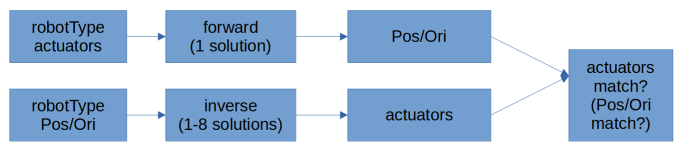
The kinematics code includes code to test the robot type's code for forward and inverse kinematics. It can be run with simulation with random values of actuator angles or by G-Code G1 target positions and orientations with M669 R ... (tbd to be specified).
The procedure is as follows:
- a robotType (type, configuration of actuators, arms etc) is specified
- with random actuator angles or positions (for rotary or prismatic actuators), forward position and orientation is calculated
- with this position/orientation, the inverse solution(s) are calculated
- the match is tested, primarily the actuator match. Position/Orientation match can also be tested to test for rounding errors or singularity reasons to hinder reachability
- the testing can also be other round, calculating the inverse first and then validating it by calculating foward after it
Additional idea:
- for existing kinematics, take forward/inverse code and compare the results it with Screw/GA code solutions. Allows to check implementation of options also (tilting parameters etc).
¶ CGA storage
CGA, conformal geometric algebra, uses 32 values for every object (following named 0...31), but not all at the same time and not at the same places. To store and use efficient, the following storage methods are used:
- cgaObject: 1 byte char for object type and 4 byte size_t to bitwise mark which 0...31 values are used for this object. Stored as array, growing if necessary. Object type is numbered by the index number. An enum list will list the object names and properties.
- idx32ToPatt: lookup from 0...32 to the char pattern.
- pattToIdx32: lookup from int(char-patt), which is 0...32, to the index of 0...32. The normal 0...31 values are stored mirrored to idx32ToPatt, value 32 is used to represent 0.
Patt and idx32 have different orders, hence the lookup-tables: while idx32 is ordered according to the table about blades on the GA page (and is the numbering of Gaalop), pattern is ordered logically as described below.
Gaalop doesn't differ between a 0 result and a scalar result of value 0. The pattern 0b00100000 is added in this firmware for a 0 value, so the code can differentiate between a 0 result and a scalar result of value 0.
Bytes needed: 5 * number of objects/transformations. + 33 + 33. About 200 bytes in total.
- the objects are stored as 1-byte object type and a float array of the used 0...31 values. Example: a point is specified by the cgaObject type 1 and an array of floats for the used values, i. e. 5 values (all 1-blades).
- pattern is stored as bits from right side (LSB-0), starting with e1. The 6th bit marks 0, i. e. no 0...31 pattern result. Example 0b00011001 is e1info with int(patt)=25 and idx=21. 21 means bit position 22 in the 0...31 array of the values of the variable.